I believe in order to understand something you need to be able to explain it to somebody else.
In that light here is me helping you helping me. I will try
and do this for other data structures and algorithms.
Binary search is a search method for searching in a ordered list. Order in this sense meaning the list has a hierarchy that might be purely numeric/temporal but it also could be lexicographical like alphabetical ordering.
How does it it work?
Here is the pseudocode
left = 0
right = length of array - 1
while left <= right
mid = rounded middle of (left + right) / 2
if mid = target return mid
if mid > target right = mid -1
if mid < target left = mid +1It seems simple enough right? Another way to think of this is we are taking the list checking the middle if the middle is larger we look at the two sub arrays and do the same depending if the middle is larger or smaller.
Worked Example
Let’s say we are looking for 19
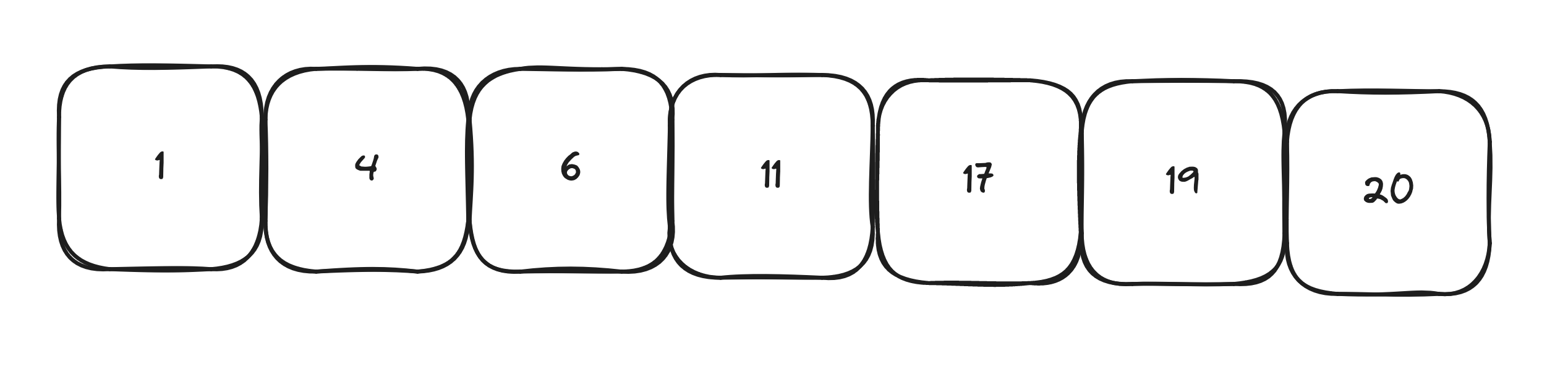
Let’s now add the pointers
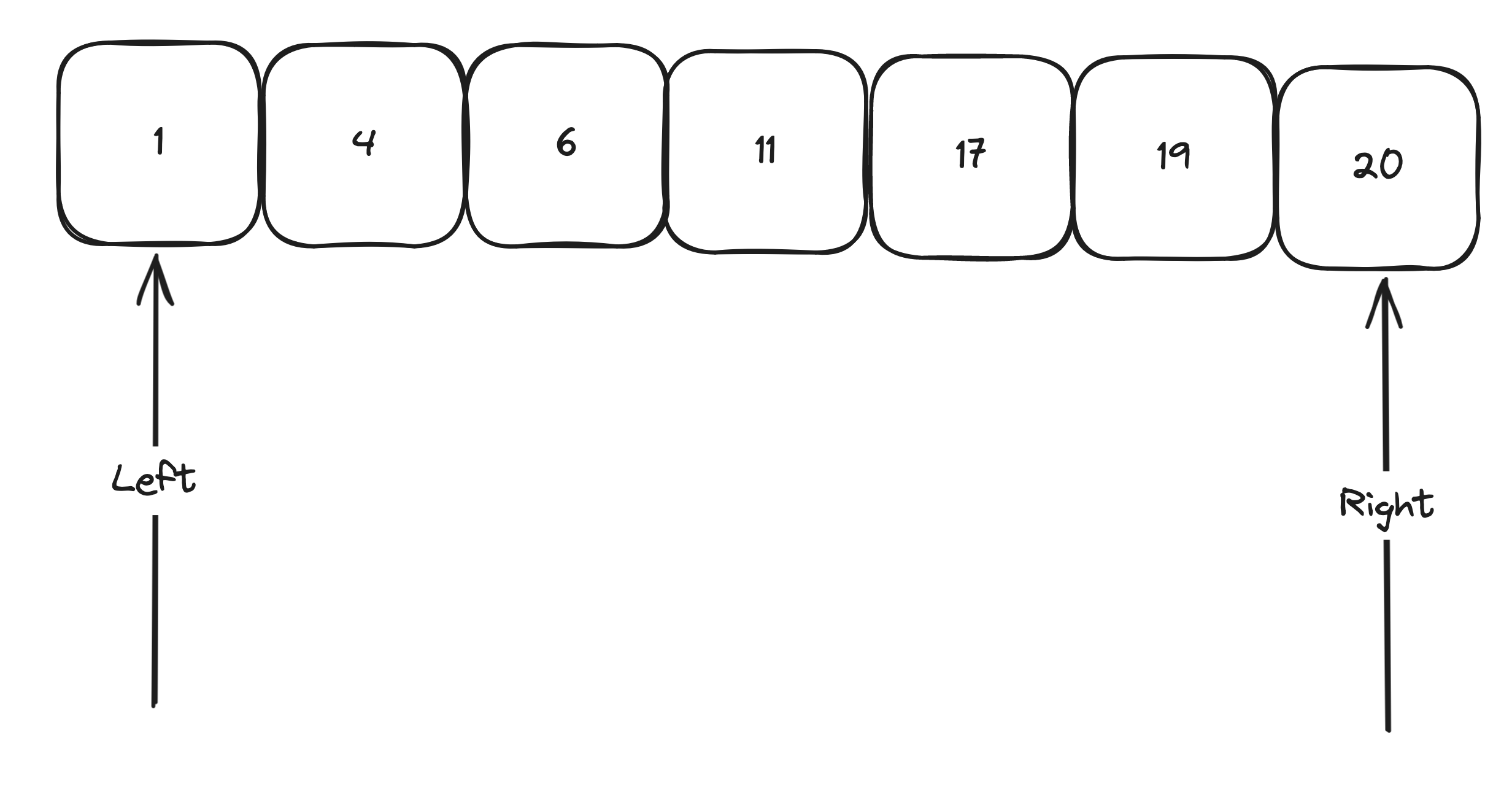
Now let’s add the mid in python //2 will round up

Since 11 is less than 19 we now make left 17 since we do mid + 1
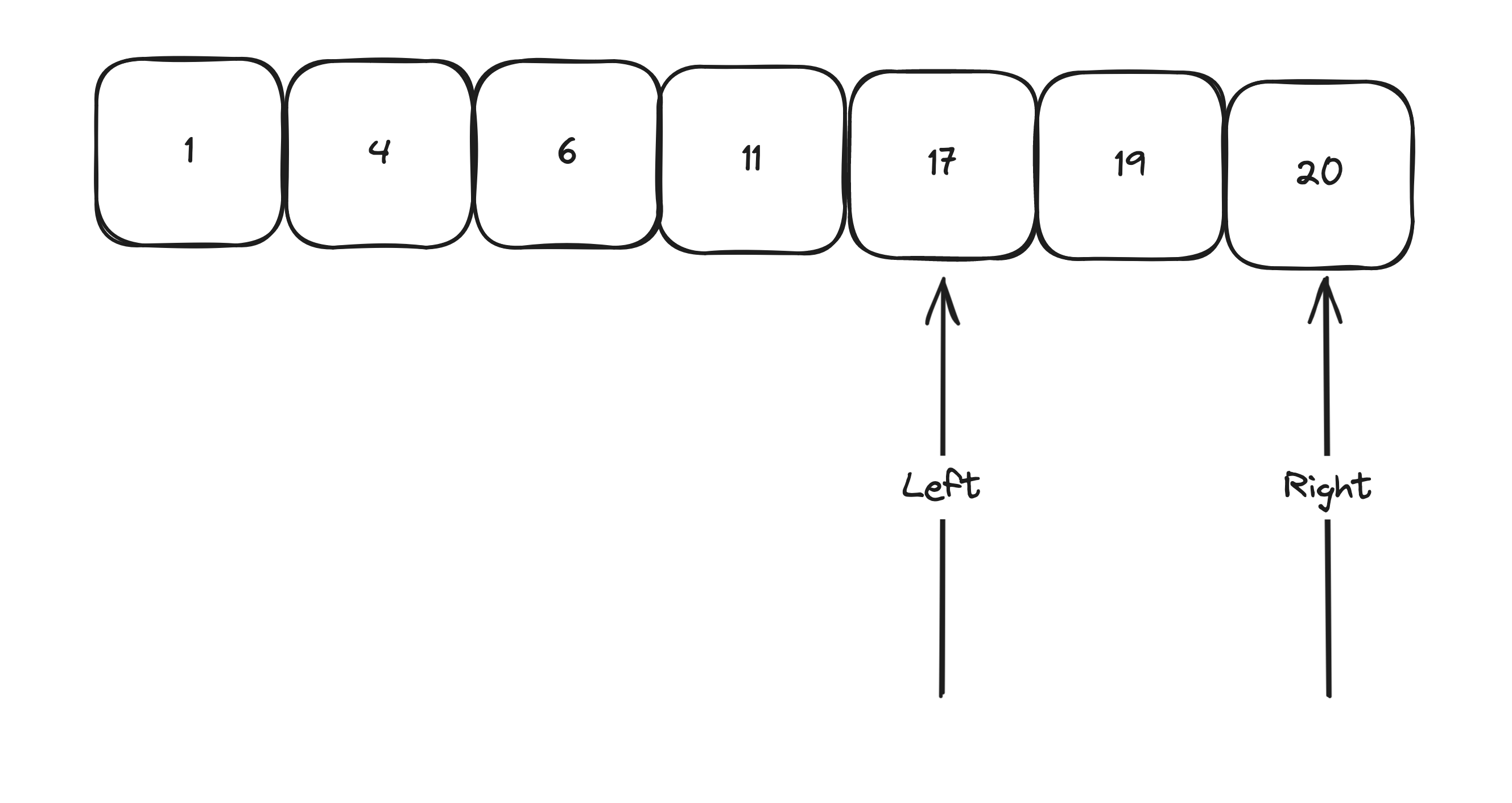
Now let’s add mid

Since we have not reached the target we can exit.
Time/Space complexity
The time complexity for this problem is O(log(n)) and the space complexity is O(1), The reason the time complexity is Log is because we are taking half the array each time. The space complexity is constant, because we are not requiring any additional data to be stored beyond the pointers to left right middle.
FAQ’s
Does the array need to be ordered to work? Yes, though the algorthm will “run” it won’t be possible to get the right answer because a random ordering will mean it would not be able to arrive at the answer.
If the array is unordered wound’t it make sense to sort and search or search the list directly in a brute force manner? Excellent question If we use a sorting method like merge sort(my favourite due to it’s consistent performance) that would mean O(nlog(n) to sort + O(log(n) in computer science we would resolve this to O(nlog(n) this is greater than O(n) which is the brute force way of searching an array, meaning sorting and searching would be slower.